Bir Möbius şeridinin kaç yüzü vardır?
Bachelard'ın kitabını öylesine çarpıcı bulmuşum ve kitaptan öylesine etkilenmişim ki, aradan yıllar geçmesine karşın bugün bile birçok bölüm tümüyle kafamda...

Gaston Bachelard, 1884 − 1962 yılları arasında yaşamış bir Fransız filozofudur. Psikanaliz ve bilim felsefesindeki çalışmalarıyla tanınır. Bilimsel Kafanın Oluşması adlı yapıtında hem kişide hem de tarihte bilimselliğin oluşmasını inceler. Savına göre bu oluşum sürekli değildir, bilimsellik yavaş yavaş oluşmaz. Tam tersine sıçramalar ve kopmalarla oluşur.
Bilimsel düşüncenin gelişmesinin önünde türlü engeller vardır. Bu engel- ler doğrudan bilimle ilgili değildirler, psikoloji ve düşünce düzeyinde engellerdir; bilimin kendisinden değil, kişiden ve kişinin yaşadığı çağdan kaynak- lanırlar. Bachelard engellerin birdenbire aşıldığını savunuyor. Sava ister katılın ister katılmayın, Bachelard büyük bir ustalıkla işlemiş konuyu. Üstelik bir macera romanı kadar heyecanlandırıcı ve sürükleyici kitap.
Kitabı öylesine çarpıcı bulmuşum ve kitaptan öylesine etkilenmişim ki, aradan yıllar geçmesine karşın bugün bile birçok bölüm tümüyle kafamda.

Gaston Bachelard
Bachelard kitabının bir bölümünde 18’inci yüzyıl biliminin ilgi çekmek için şaşırtma ve meraklandırma yolunu seçtiğini ve bunun bilimin zararına olduğunu söylüyor.
Örneğin Volta, elektrikli tabancasını yüzlerce sayfada anlatmış. Elektrikli tabancanın ne olduğunu bilmiyorum ama çok basit bir aygıt olmalı. Bu basit aygıta Volta, elektrikoflogopnömatik tabanca adını vermiş... Bu korkunç adı duyanlar, bu da neymiş diye merak edip Volta’nın buluşuyla ilgilenecekler sözümona. Sonra da, "Volta’nın elektrikoflogopnömatik tabancısı bir harika! Bilim baş döndürücü bir hızla gelişiyor, izlemesi kolay olmuyor" deyip birbirlerine fiyaka yapacaklar. (Bilimin fiyaka yapmak istemesi Bachelard’a göre bilimin önünde bir başka engel.)
Bu bölümden biraz alıntı yapmak istiyorum:
"İlgilendirmek için sistemli olarak şaşırtmak isteniyor. Çelişkili gibi görünen deneyler sunuluyor. Bir su fışkırtmasıyla alkollü likörlerin ateş alması 18’inci yüzyıl biçeminde Gordon’un güzel bir deneyidir. Bunun gibi, Priestley’in anlattığına göre Dr. Watson bir buz parçasıyla şarabı alevlendirmiş.
Ateşin suyla ya da buzla yakılabilmesi gibi deneysel çelişkilerle doğanın gizemli karakterinin ortaya çıkarıldığı sanılıyor. [...] 18’inci yüzyılın bir tek bilimsel kitabı yoktur ki, bu bilinemezlik uçurumu önünde zihinleri titretmeye zorunlu olduğunu sanmasın, bilinmeyenin derinliğinde başımızı döndürmeye çalışmasın!"
Çok derin düşünceler onlarca örnek verilerek ve okurun sıkılmasına olanak verilmeden sunulmuş. Meydan-Larousse, Bachelard’ın bir fotoğrafını basmış. Yüzü de düşünceleri gibi apaydınlık. Sözünü ettiğim kitabın Türkçe’ye çevrildiğini sanmıyorum. Büyük bir eksiklik.
Buraya değin yazdıklarım bundan sonra yazacaklarıma bir eleştiridir. Çünkü bundan sonra amacım okuru şaşırtmak, matematiği sihirbazlık gibi göstermek. Bunu yapmamam gerektiğini biliyorum ama dayanamadım.
Elinize bir kâğıt şeridi alın (Şekil 1.) Bu şeridin iki yüzü vardır. Bir yüzünü maviye, öbür yüzünü kırmızıya boyayabilirsiniz. Daha şaşılası bir şey söylemedim. Şimdi şeridin bir ucunu sabit tutup öbür ucunu 180 derece döndürün (Şekil 2) ve AD ile CB kenarlarını A ile C köşeleri ve B ile D köşeleri üstüste gelecek biçimde yapıştırın (Şekil 3). Böylece bir Möbius şeridi* elde etmiş olursunuz.
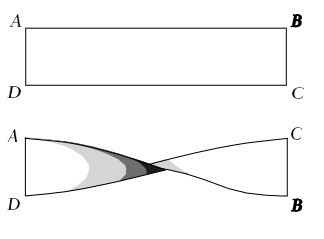
Şekil 1 ve 2.

Şekil 3.
Möbius şeridinin kaç yüzü vardır? İki gibi gözüküyor değil mi? Peki, iki yüzü olduğunu varsayalım.
O zaman bir yüzünü kırmızıya, öbür yüzünü maviye boyayabilirsiniz. Deneyin. Başaramayacaksınız (Şekil 4.)

Şekil 4.
Başaramayacaksınız, çünkü Möbius şeridinin iki değil bir yüzü vardır. Yani yürüyerek ve cambazlık etmeden Möbius şeridinin önünden arkasına geçebilirsiniz.
Ayrıca Möbius şeridinin bir kenarı vardır. Bir kenarı durmadan izlerseniz, başladığınız yere dönersiniz.
Matematikçilerin buluşları elektrikoflogopnömatik tabancadan daha basittir.
Şimdi Möbius şeridinin ortasından uzunlamasına bir çizgi çizin. Möbius şeridinin tek yüzü olduğundan, elinizi hiç kaldırmadan başladığınız yere geri döneceksiniz.
Bu çizgiyi izleyerek Möbius şeridini kesin. Kaç şerit elde edeceksiniz dersiniz?

İki mi?
Yanlış! Bir! Hem de iki yüzlü bir şerit! Bir yüzünü kırmızıya, öbürünü maviye boyayabilirsiniz.
Daha bitmedi. Yeni bir Möbius şeridi yapın. Bu kez çizgiyi ortadan değil şeridin üçte birinden çizin. Elinizi hiç kaldırmadan dümdüz, kenarlara koşut olarak çizmeyi sürdürürseniz, şekilde de görüldüğü gibi yanyana iki çizgi elde edeceksiniz.
Şimdi bu çizgiden kesmeye başlayın. İki şerit elde edeceksiniz. Büyüğünün iki, küçüğünün bir yüzü vardır. Yani bu nesnenin toplam üç yüzü vardır.

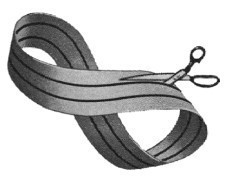
Möbius şeridi, Escher sayesinde sanata da yansımıştır. (Escher’in sanatı da arada bir matematiğe yansır.)
Yazımızı Escher’in bir Möbius şeridi resmiyle noktalayalım.

* August Ferdinand Möbius (1790-1868) Alman astronom ve matematikçisidir. En çok Möbius şeridiyle tanınır. Ama Möbius dönüşümleri ve grupları daha önemli buluşlarıdır.









