Tavla ve Bilimsel Düşünce
"Bakalım siz tavlayı nasıl oynuyorsunuz? Önce birkaç kolay soruyu yanıtlayın."

Yıllar önce çok satan bir gazetemiz Türkiye Tavla Şampiyonası düzenlemişti. Bizde tavlacı çok. İş yerlerinde bile tavla oynanır. Bileğine güvenen katıldı şampiyonaya. Ne de çok bileğine güvenen varmış! "Kemik"e ve talihe sövgülerin yağdığı ve "Pencüse, şaşırdı gencüse" (her ne demekse) gibi tekerlemelerin bol bol kullanıldığı elemeler yapıldı. Önce kıraathanelerin şampiyonları belirlendi, sonra sırasıyla köylerin, kasabaların ve ilçelerin, arkasından da illerin. Pek zorlu maçlar sonunda il şampiyonları arasından Türkiye birincisi seçildi. Türkiye birincisi yurtdışında bir yerde, galiba ABD’de, dünya şampiyonasına katıldı. "Eh artık, tavlada da dünya şampiyonu oluruz" diyordum. Gece gündüz yaz kış demeden 7’den 70’e tavla oynayan bir milletiz. Şampiyonluk hakkımızdır diye düşünüyordum. Beklediğim çıkmadı. Elendik... Gazetede bir söyleşi yayımlandı elenen şampiyonumuzla. Sanki erkekliği söz konusuymuş gibi kükrüyordu:
- Adam ceharıdü oynayacak... Bekle, bekle... 15 dakika düşündü... 15 dakika! Sinir mi dayanır! Satranç mı oynuyoruz tavla mı?
Neredeyse, yenilmiş olmasına aldırmadan, "Adam tavla bilmiyor, tavlada çok geri bu ecnebiler," diyecek.
Bakalım siz tavlayı nasıl oynuyorsunuz? Önce birkaç kolay soruyu yanıtlayın.
Birinci Oyun. Aşağıdaki birinci oyunda siyahsınız. Beyaz toplamaya çoktan başlamış bile, dört pulu kalmış kala kala. Şeşbeş (6-5) attınız. Nasıl oynarsınız?
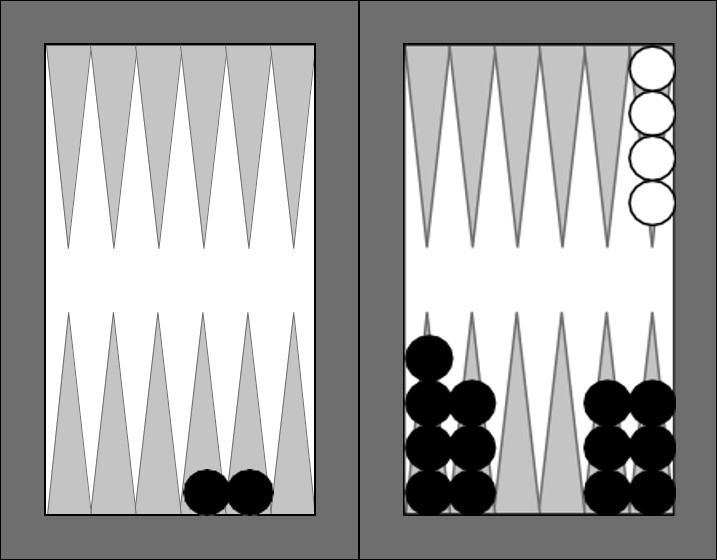
Sakın alışkanlıkla se (3) kapısını almaya kalkmayın... Yoksa bir sonraki zarınız dörtcehar (4 - 4) olursa mars olursunuz. Hem de hiç gereği yokken... Dörtceharı kötü bir zar olmaktan kurtarabilirsiniz. Se kapısını alacağınıza, en uzaktaki pulu 5 oynayarak cehar hanesine yatın. Böylece rakibinize çift gelmedikçe mars olmazsınız. Üstelik bu oyunu oynamanın hiçbir sakıncası yoktur.
İkinci Oyun. İkinci soruya geldik. İkinci oyunda durumunuz gene iyi değil. Aşağıdaki oyunda siyah pullarla oynuyorsunuz ve sanki atacak başka zar yokmuş gibi 2 - 1 attınız. Nasıl oynarsınız?
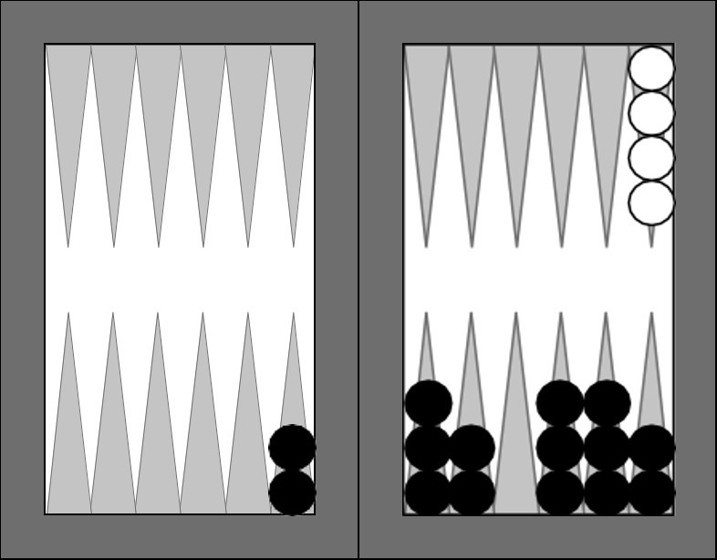
Geçen oyunun benzeri bu oyun da. Sakın iki pulunuzu birden içeri sokmaya kalkmayın. Yoksa bir sonraki zar atışınızda dört - cehara mars olursunuz. Dışarıdaki iki puldan birini dört hanesine yatın. Rakibiniz çift atmadıkça mars olmazsınız.
Alışkanlıkla değil düşünerek oynamalı.
Üçüncü Oyun. Bugün sizin gününüz değil. Aşağıdaki durumda, sanki parasını vermiş gibi gene 2 - 1 attınız. Nasıl oynarsınız?
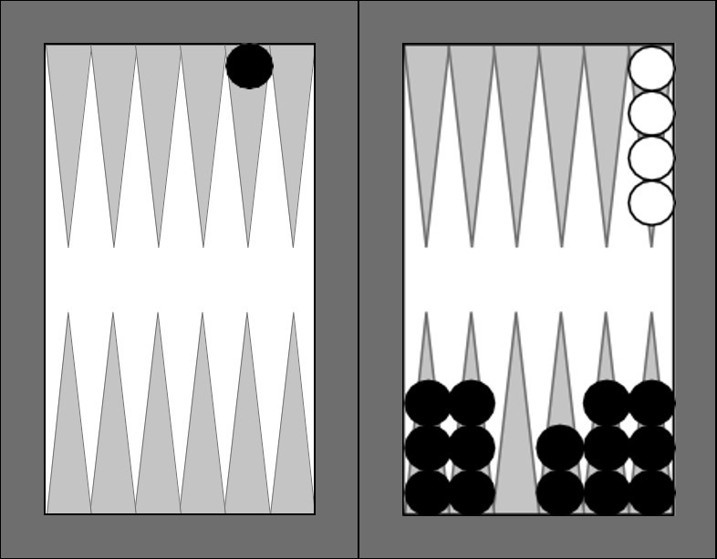
Sakın dışarıdaki pulunuzu, "iki, bir daha üç eder" diyerek yanaşayım demeyin. Dört ceharı (4 - 4) düşünün. Eğer dört cehara da marstan kurtulmak istiyorsanız dışarıdaki pulunuzu iki yanaşın (böylece düsseyle (3 - 3) de marstan kurtulabilirsiniz) ve 1’i içerden oynayıp dört hanesine yatın (böylece dört cehara da marstan kurtulursunuz.) Dediğimi yaparsanız mars olmama olasılığını artırırsınız ve bir şey kaybetmezsiniz.
Dördüncü Oyun. Durmadan yeniliyorsunuz ve doymak bilmiyorsunuz. Aşağıdaki durumda şeşiyek (6 - 1) attınız. Nasıl oynarsınız?
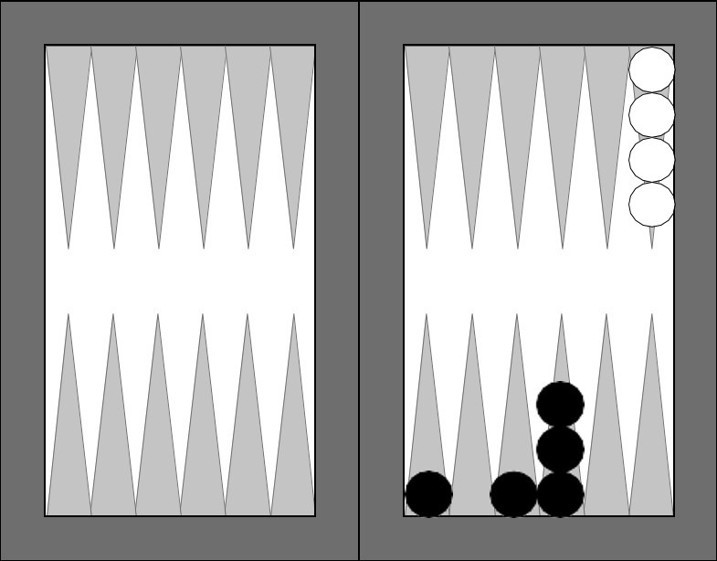
Artık düşünmek gerektiğini biliyorsunuz. Şeşi oynamak kolay. Zorunlu olarak 6 hanesinden alacaksınız. Peki, yeki nasıl oynamalısınız? Oyunu kazanmak için bir çifte gereksiniyorsunuz. Demek ki dört hanesindeki pulu üç hanesindeki pulların üstüne koymalısınız. Böylece düsseyle (3 - 3) oyunu kazanabilirsiniz.
Eğer böyle oynayıp da düsseyle oyunu kazanırsanız, kimsenin size şanslısın demeye hakkı yoktur. Çünkü o şansı kendinize siz yaratıyorsunuz.
Ve öyle oynamayıp düsse atarsanız ve oyunu kaybederseniz, şanssızım diye dövünmeye de hakkınız yoktur.
Şimdi daha zor durumlara göz atalım. Önce biraz olasılık hesaplayalım. Zarların cıvasız ve hilesiz olduğunu varsayacağız. Her zarın 6 yüzü vardır. Her yüzün gelme (yani her "olay"ın gerçekleşme) olasılığı birbirine eşittir. Ve toplam olasılık 1 olmalıdır1. Demek ki bir tek zar atıldığında her yüzün gelme olasılığı 1/6’dır.
İki zarda olasılıklar nelerdir? Birinci zar için 6, ikinci zar için de 6 tane olası olay vardır. Yani iki zarda 6 × 6 = 36 tane olası olay vardır:
1 − 1 1 − 2 1 − 3 1 − 4 1 − 5 1 − 6
2 − 1 2 − 2 2 − 3 2 − 4 2 − 5 2 − 6
3 − 1 3 − 2 3 − 3 3 − 4 3 − 5 3 − 6
4 − 1 4 − 2 4 − 3 4 − 4 4 − 5 4 − 6
5 − 1 5 − 2 5 − 3 5 − 4 5 − 5 5 − 6
6 − 1 6 − 2 6 − 3 6 − 4 6 − 5 6 − 6
Bu olayların her birinin gerçekleşme olasılığı birbirine eşittir. Toplam olasılık 1 olması gerektiğinden, bu 36 olayın her birinin gerçekleşme olasılığı 1/36’dır.
Ama bunlar, iki zarı birbirinden ayırt ettiğimizdeki olasılıklardır. Tavlada "birinci zar", "ikinci zar" diye bir ayrım yapılmaz. Örneğin 5 - 2 ile 2 - 5 arasında bir ayrım yoktur. Bu yüzden pencüdü gelme olasılığı 1/36 değil, 2/36’dır, yani 1/18’dir. Ama dörtceharın (4 - 4) olasılığı 1/36’dır. Genel olarak, hilesiz iki zarla belli bir çiftin gelme olasılığı 1/36’dır, çift olmayan belli bir zarın gelme olasılığıysa 2/36’dır.
Alıştırma olarak aşağıdaki durumda siyahın beyaz pulu kırma olasılığını hesaplayalım.
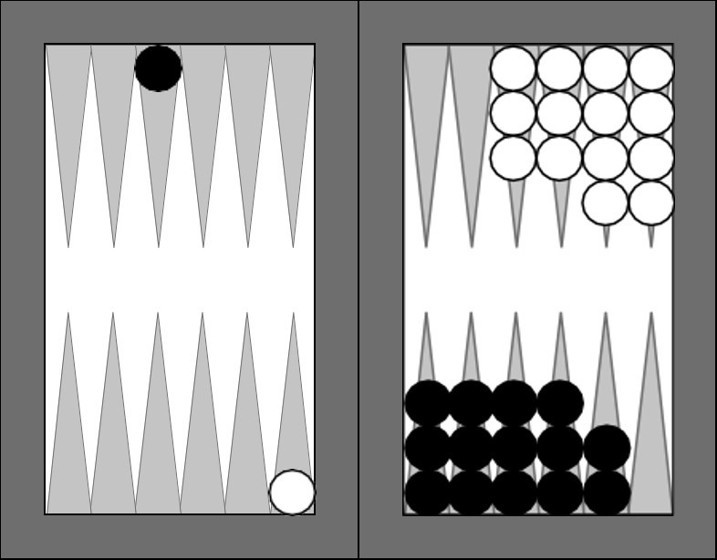
Kıracak zarları sıralayalım: 2 - 2, 6 - 2, 5 - 3, 4 - 4. Bu zarların olasılıkları sırasıyla
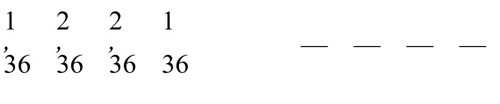
olur. Dolayısıyla siyahın beyaz pulu kırma olasılığı
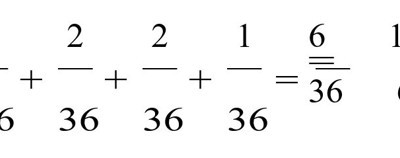
olur.
Aşağıdaki durum şampiyonumuzun kaybettiği maçtan bir görüntü olabilir. Durum 4 - 4 beraberler. Şampiyonumuz siyah pullarla oynuyor. Karşı taraf iki pul dışında bütün pullarını toplamış. Şampiyonumuz, bir biçimde, bu iki pulu kırmış. Karşı taraf dört ceharı (4 - 4) oturtmuş. Şampiyonumuzun ne attığı önemli değil. Aşağıdaki duruma erişilmiş. Bu durumda karşı taraf (beyazlar) ceharıdü (4 - 2) atmış. Ve işte o zaman 15 dakika düşünmüş. Nasıl oynamalı?
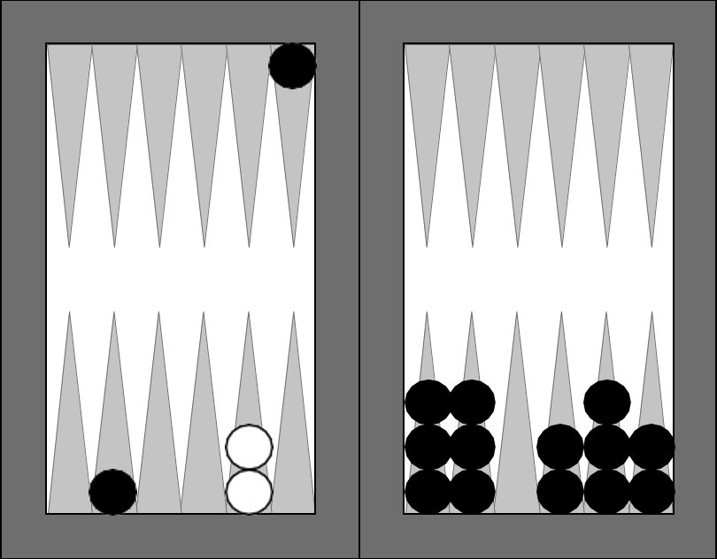
Doğrusu zor bir durum. Benim diyen tavlacı kolay kolay karar veremez. Beyazın amacı ne? Durum 4 - 4 olduğundan marsa değil oyuna oynamalı. Pullarından yalnız biri kırılsa, oyunu kazanabilir. İkisi birden kırılırsa kazanma olasılığı gene var ama daha düşük.
Beyazın iki seçeneği var. Ya iki pulunu birden oynayacak (birini 2, öbürünü oynamalı?
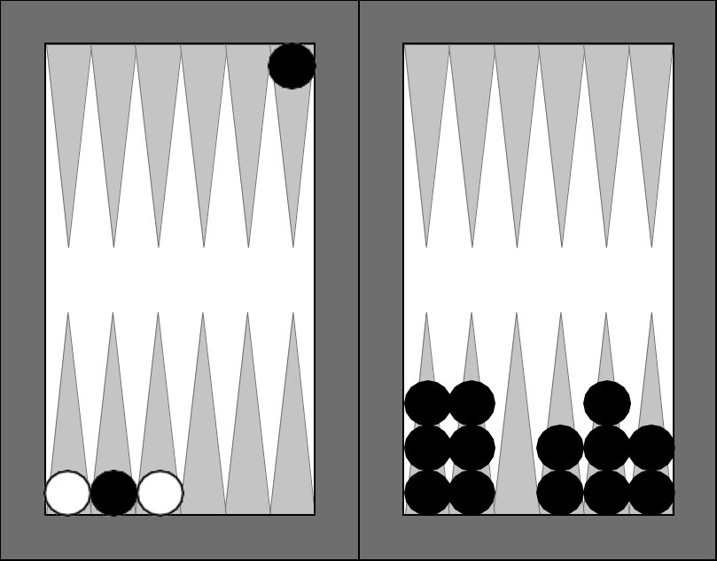
Diyelim birincisini seçti. Durum yukarıdaki gibi.
Bu durumda şampiyonumuzun kırma olasılığını hesaplayalım:
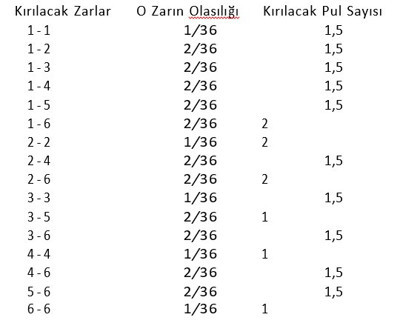
Yukarıdaki tabloda kırılacak pul sayısını da gösterdik. Eğer siyahlar birinci oyunda salt bir pul kırabiliyorsa, ama bir sonraki oyunda ikinci pulu da kırma olasılığı varsa, kırılan pul sayısına 1,5 dedik.
Şimdilik kırılacak pul sayısını dikkate almayalım. O zaman şampiyonumuzun en az bir pul kırma olasılığı yukarıdaki olasılıkların toplamıdır, yani 27/36, yani tam tamına 3/4’tür.
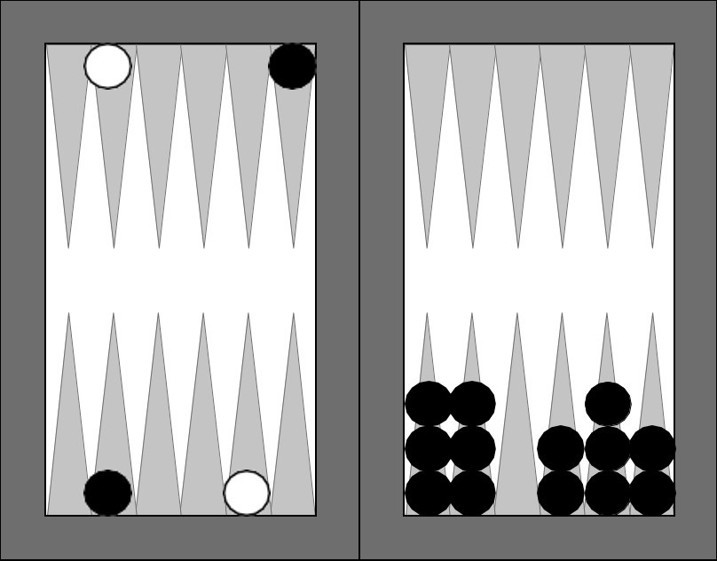
Şimdi karşı tarafın ikinci seçeneği yeğlediğini varsayalım. Bu varsayımla erişilen durum yukarıda. Bu ikinci şıkta şampiyonumuzun kırma olasılığını hesaplayalım:
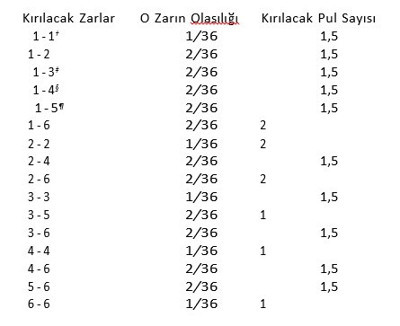
Bu durumda şampiyonumuzun en az bir pul kırma olasılığı bu olasılıkların toplamı, yani 25/36’dır.
Demek ki eğer beyaz ikinci oyunu seçerse daha az bir olasılıkla (25/36’ya karşı 27/36 olasılıkla) kırılacaklar. Bu sayılar göz önünde tutularak beyazın ikinci oyunu seçmesi gerektiği öne sürülebilir.
Ama tavla o denli kolay bir oyun değil. Beyaz, bir kırıkla oyunu kazanabileceğini düşünebilir ve pek de haksız olduğu söylenemez. Beyaz bu durumdan bir kırıkla kurtulabilirse, oyunu kazanma olasılığı küçümsenemez. Kolay kolay karar verilecek bir durum değil. Her ustanın değişik bir görüşü olabilir. Bu satırları yazan ustaya göre birinci seçeneğin kazanma şansı daha yüksektir.
Bu gibi durumlarda bilgisayardan yararlanılabilir. Oldukça iyi tavla oynayan bir bilgisayara yukarıdaki durum verilir. Beyaza bir milyon kez birinci oyun, bir milyon kez ikinci oyun oynattırılır. Sonra da beyazın en çok hangi oyunu oynadığında kazandığına bakılır.
Tavla gibi basit bir oyunun bile bilimi yapılmalı, kitapları yazılmalı. ABD’de tavla oldukça yeni bir oyun olmasına karşın, tavla üzerine onlarca kitap vardır. Yüzyıllarca tavla oynanan, tavla ustasından geçilmeyen ülkemizdeyse bir tek tavla kitabı yazılmamıştır. Üzerinde düşünülmesi gereken bir olgu2.
Bu yazıyı yazdıktan sonra babam meydan okudu:
– Gel bakalım, göstereyim sana şansın tavladaki payını!
– Aman baba, yapma etme, beni tavlada kimse yenemez...
Oynadık ve 5 - 0 yenildim.
– Hani seni kimse yenemezdi?
– Demek bir sen yenebilirmişsin...
– Yazın iyi olmamış. Eksik kalmış.
Neyi eksik bıraktığımı anlattıktan sonra tehdit etti:
– Bunu yazına eklemezsen, karşı yazı yazarım, rezil olursun...
Bunun üzerine okuduğunuz bu paragrafı ve aşağıdakini ekledim.
Gördüğümüz gibi 4 - 4 gelme olasılığı 1/36’dır. İki kez üst üste 4 - 4 gelme olasılığıysa (1/36)2, yani 1/1296’dır. Oldukça düşük bir olasılık. Bu birinci nokta. Öte yandan, bir kez 4 - 4 attıktan sonra, ikinci kez gene 4 - 4 gelme olasılığı gene 1/36’dır. Zarlar gerçekten hilesizse, daha önceden 100 kez 4 - 4 atmışsanız, 101 kez 4 - 4 atma olasılığı gene 1/36’dır. Başka bir deyişle "zarların belleği yoktur".
İşte babama bu yüzden yenildim.
1Matematikte olasılıklar üzerine hesaplanır. Günlük dilde kullandığımız "yüzde yüz"e matematikte "1 olasılıkla" denir. %25, matematik dilinde 1/4’tür. %30 ise 3/10’dur. Zarın yüzlerinden biri kesinlikle geleceğinden toplam olasılık 1 olmalıdır.
†Bu zarla en iyi oyun üç oynayarak alttaki beyaz taşı kırmak ve dü hanesindeki taşı yek hanesine taşımaktır.
‡Hepyek gelmiş gibi yukarıdaki öğütü dinleyin!
§Nasıl oynarsınız?
¶Nasıl oynarsınız?
2TÜBİTAK’ın yayımladığı Bilim ve Teknik dergisinde artık bir Tavla Köşesi var. Ayrıca, bir de tavla kitabı Almancadan Türkçeye çevrilmiş. Tavlayı da Batılılardan öğreniyoruz! Bkz. Kaynakça [2].









