Düğüm: Matematiğin ilginç problemi
Düğümler kuramı matematiğin çok güzel ve heyecanlı dallarından biridir.

Ali NESİN
Aşağıda iki düğüm görüyorsunuz:
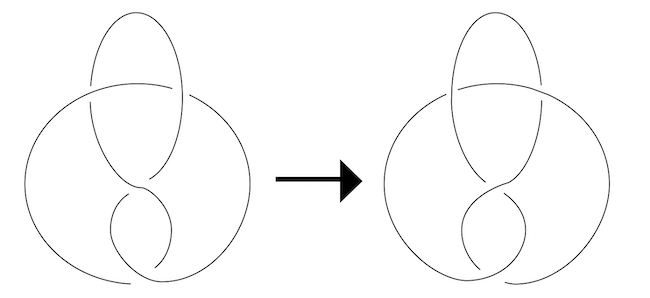
Bu iki düğüm birbirinin aynı gibi görünüyorlar. Öyle mi gerçekten? Dikkatlice bakarsanız, bu iki düğümün birbirinin tıpatıp aynı olmadığını görürsünüz.
Düğümlerden biri, öbürünün aynadaki görüntüsü, ama aynısı değil...
Birinden öbürünü, kesip biçmeden, yalnızca iple oynayarak (örneğin ipi döndürerek) elde edebilir miyiz?
Evet. Yani aslında bu iki düğüm aynı düğümdürler. Uzayda iple oynayarak birini öbürü yapabiliriz.
Düğümlerden birini 180 derece döndürürseniz, öbür düğümü değil, gene aynı düğümü elde edersiniz, demek ki düğümlerden birini 180 derece döndürmek yetmiyor.
Aşağıdaki şekildeki soldaki düğümden başlayalım (Şekil 1). Üstteki halkayı sağa yatıralım (Şekil 2 ve 3). Sonra soldaki halkayı sağa yatıralım (Şekil 4 ve 5). Düğümü, yelkovanın yönüne doğru 90 derece döndürelim (Şekil 6). Yukardaki ikinci düğümü elde ettik.
Düğümler kuramı matematiğin çok güzel ve heyecanlı dallarından biridir. Dört ve daha yüksek boyutlarda her düğüm birbirinin eşidir; dört ve daha çok boyutlu uzaylarda, düğümü çözecek bol bol yerimiz (zamanımız!) vardır. Oysa üç boyutlu uzayda birbirinin eşi olmayan birçok düğüm vardır. Bu düğümlerin sınırlandırılması matematiğin ilginç problemlerinden biridir.
Düğümler kuramı hakkında daha fazla bilgi edinmek için, Crowell ve Fox’un 1963’te yayımlanmış ve bugün bir klasik olarak kabul edilen Introduction to Knot Theory’ye (Ginn and Company) bakabilirsiniz.









