Satranç tahtası soruları
Satranç tahtasının güzelliği mantığa da yansır. Olağanüstü güzel satranç tahtası problemleri vardır.

Ali NESİN
Satranç güzel bir oyundur. Salt oyun olarak değil, oyunun tahtası ve askerleri de güzeldir. Örneğin bir at... Ben atı çok estetik bulurum. Herkes atı beğeniyor olmalı ki, at satrancın simgesi haline gelmiştir. Satrancın atı mı yoksa keman mı daha güzeldir? Karar veremem, her ikisine de bayılırım.
Askerlerini bir yana bırakırsak, satranç tahtasının kendisi de güzeldir. Banyo ve mutfaklarımızı bu güzel biçimle süslemez miyiz?
Usta zanaatkârların yaptığı satranç takımları çok pahalıya satılır. O takımlarda satranç oynanmaz ama olsun, güzelliği yeter. Ben yine de uluslararası yarışmalarda kullanılan basit satranç takımlarını yeğlerim. Yalınlıkta ve güzellikte üstüne yoktur.
Satranç tahtasının güzelliği mantığa da yansır. Olağanüstü güzel satranç tahtası problemleri vardır. Bildiklerimden birikisini sunuyorum:
Birinci Problem: Bilinen bir problemdir: Bir satranç tahtasının en üst sağ karesiyle en alt sol karesini kesip attığınızda, satranç tahtasının geri kalan 62 karesini, herbiri iki kare kaplayan dominolarla kaplayabilir misiniz?

Yanıt olumsuzdur, yani "kaplayamam"dır.
Yanıtın Kanıtı: Satranç tahtasının en üst sağ karesiyle en alt sol karesi aynı renktedirler. (Siyah karelerdir. Siyah kare daima sol alt köşede bulunmalıdır. Yoksa usta satranç oyuncuları huylanırlar.) Dolayısıyla, dominoyla kaplamamız gereken tahtada artık 32 beyaz kare ve 30 siyah kare kalmıştır. Oysa her domino bir siyah ve bir beyaz kare kaplar, yani dominoların kapladığı karelerin yarısı siyah, yarısı beyaz olmalıdır. Demek ki dominolarla 32 beyaz ve 30 siyah kare kaplanamaz.
Bu problem salt 8 x 8 satranç tahtası için değil, n x n boyutlu her satranç tahtası için sorulabilir. Yanıt her seferinde "hayır"dır.
Öte yandan, 8 x 8 boyutlu bir satranç tahtasından bir siyah, bir beyaz kare kesilirse, o satranç tahtası dominolarla kap- lanabilir. Şöyle. Önce kesilmiş satranç tahtasına aşağıdaki gibi iki tarak yerleştirin:
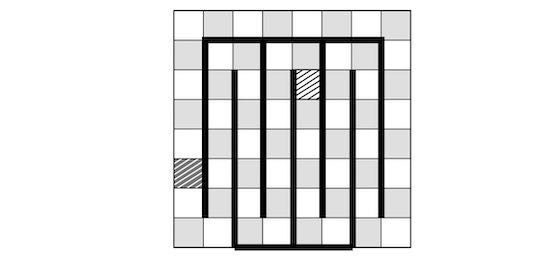
Bu taraklar satranç tahtasında bir labirent gibi koridorlar açıyorlar. Koridorları takip ederek, bir eksik kareden, öbür ek- sik kareye iki türlü gidebiliriz. Nasıl gidersek gidelim, her iki yolda da çift sayıda kareden geçeriz. Köşeler de bir sorun ya- ratmadığından, dominoları tarakların açtığı koridorlara yerleştirerek, satranç tahtasını dominolarla kaplayabiliriz.
İkinci Problem: Bu soruyu adlı kitabımda da sormuştum, yineliyorum. Önünüze bir satranç tahtası alın. En üstteki sol kareye bir tavla pulu koyun. O pulla şu hamleleri yapabilirsiniz: Pulu bir kare sağa, sola, aşağı ya da yukarı kaydırabilirsiniz. Her kareden geçerek ve her kareden yalnızca bir kez geçerek pulu en alt sağ kareye götürebilir misiniz?
Götürebilirseniz nasıl götürürsünüz, götüremezseniz neden götüremezsiniz?
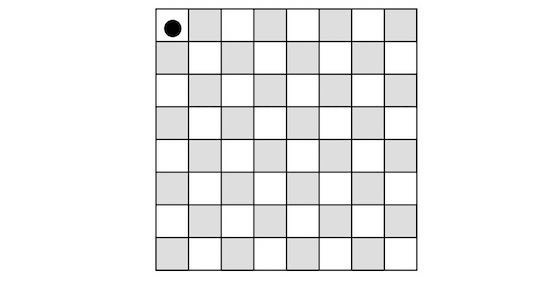
Doğru yanıt... "Hayır götüremem"dir. Niye mi? Satranç tahtasında 64 kare vardır. Her kareden bir kez geçmemiz gerektiğine göre 63 hamle yapmalıyız. Yani 63 hamlede en üst sol kareden en alt sağ kareye gitmeliyiz. Oysa bu iki kare beyaz. Ve tek sayılık hamlede beyaz bir kareden gene beyaz bir kareye gidilemez!
Yanıt şaşırtıcı bir yalınlıkta. Elimizdeki verilerden yalnızca işimize yarayanı kullanıyoruz. Pulun hangi kareden hangi kareye gideceğinden çok, beyaz bir kareden gene beyaz bir kareye gitmesi önemli olan. Ve hamle sayısının 63 olmasından çok, bir tek sayı olması önemli. Çok daha genel ve kanıtı çok daha basit bir sonuç bulduk: Beyaz bir kareden gene beyaz bir kareye tek sayıda hamleyle gidemeyiz.
Bir de aynı soruyu bir dama tahtası için değil de, herhangi bir 8 x 8 karelik tahta için sorsaydım, yanıtı bulmak daha zor olurdu. Çünkü 8 x 8’lik tahtayı önce dama tahtası gibi boyamak gerekecekti. Sonra da yukardaki akıl yürütmeyi yapacaktık.
Üçüncü Problem: Bu problem bir satranç tahtası problemi gibi gözükmese de aslında 5 x 5’lik bir satranç tahtası problemi. 25 öğrencinin ard arda dizilmiş beşer kişilik beş sırada oturduğu bir sınıfta, öğretmen, öğrencilerin, aynı anda ya bir sağa ya bir sola ya bir öne ya da bir arkaya kayarak yer değiştirme- lerini istiyor. Her öğrenci elbette her hareketi yapamaz. Örneğin, en öndekiler öne kayamazlar. Köşedekiler sadece iki ham- le yapabilirler. Ortalarda oturanların dört değişik hamle olana- ğı var. Her öğrenci yer değiştirmek zorunda ve her öğrenci sa- dece tek bir hamle yapabilir. Öğrenciler öğretmenin dediğini yapabilirler mi? Yapamazlar.
Öne ve sola kayan öğrencilere 1 puan verelim. Arkaya ve sağa kayan öğrencilere -1 puan verelim. Öğrencilerin toplam puanı 0 etmek zorunda. (Neden?) Ama 25 tane 1 ve -1’in toplamı hiçbir zaman 0 etmez, çünkü 25 tek bir sayıdır.









