Sihirli kareler: Bütün suç Adem’le Havva'daymış!

Ali NESİN

Bir önceki yazıda, n bir tek tamsayı olduğunda n × n sihirli karelerin nasıl yapılacağını öğrenmiştik. Bu yazıda n’nin çift olduğu n × n boyutlu sihirli kareleri ele alacağız.

Her zaman yaptığımız gibi örneklerle başlayalım. Önce geçen yazıda da verdiğimiz ve sanata da yansıyan¹ünlü 4 × 4 sihirli kareyi gösterelim:

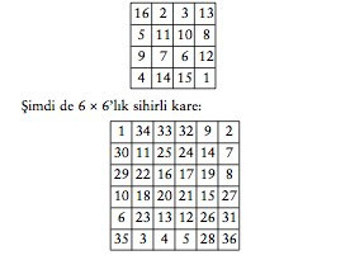
Son olarak, bu yazıda örnek olarak alacağımız 8 × 8’lik sihirli kare:

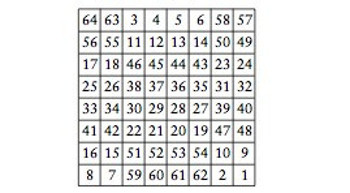
2 × 2’lik sihirli kare yok. Deneyin, neden olmadığını hemen anlarsınız: 1 sayısını bir yere koymalıyız. Orası kesin. 2’yi de bir yere koymalıyız. Ama 2 sayısını nereye koyarsak koyalım, 1’le ya aynı sıraya ya aynı sütuna ya da aynı çapraza gelecek ve sihirli toplam 1 + 2 = 3 olacak. Dolayısıyla 4’ü koyamayacağız!

Cornelius Agrippa’ya (1486–1534) göre 1 × 1’lik sihirli kare yani

karesi sonsuzluğu ve birimi (aynı anda!) simgeliyormuş. 2×2’lik sihirli karenin olmaması ise, sıkı durun, dört temel öğenin -yani hava, toprak, ateş ve suyun- yetersizliğinin kanıtıymış. Neye ye- tersizse... Cornelius sihirbaz ve büyücüdür. Büyücülük suçundan Brüksel’de bir yıl hapis yatmıştır. 3×3, 4×4, 5×5, 6×6, 7×7, 8×8 ve 9×9’luk sihirli karelerin, sırasıyla, Satürn’ü, Jüpiter’i, Mars’ı, Güneş’i, Venüs’ü, Merkür’ü ve Ay’ı simgelediklerini bulmuş ama öbür sihirli karelerin anlamlarını bulamamıştır!

Bir başka Ortaçağ "bilim adamına" göre 2×2’lik sihirli karelerin olmamasının nedeni çok daha basitmiş. Öyle bin dere- den su getirmeye gerek yokmuş... Bütün suç Adem’le Havva’daymış. Adem’le Havva yüzünden 2×2’lik sihirli kare yokmuş. Adem’le Havva ilk günahı işlemeselermiş 2×2’lik sihirli kare bal gibi de olabilirmiş.

İnsanların sihirli karelerin tılsımına kendilerini kaptırmaları nedensiz değildir. Sihirli karelerin gerçekten sihirli bir yanı vardır. Sanki sayıların biz insanlardan bağımsız bir yaşamı var- mış gibi bir duygu verir insana. Doğrusu da budur: Sayılar biz insanlardan bağımsızdır. Sayıları icat etmemiş, keşfetmişizdir, aynen Amerika’yı keşfettiğimiz gibi...

Çift kenarlı (boyutlu) sihirli kare yapmaya çalışacağız. He- men daha başlangıçtan söyleyeyim: Çift boyutlu sihirli kareleri yapmak için genel bir yöntem vermeyeceğiz, çok karmaşık. Öte yandan 4, 8, 12, 16 gibi dörde bölünebilen kenarlı sihirli kare

yapılabiliyor. Önce bu sihirli kareleri bulalım. 6, 10, 14, 18... kenarlı sihirli kareleri yazının sonuna bırakalım.

n, dörde bölünebilen bir sayı olsun. n’yi dörde bölelim ve n = 4m yazalım. Müstakbel sihirli karemizi 16 tane m × m’lik küçük kareye bölelim. Örneğin n = 8 ise (yani m = 2 ise), karemizi 16 ta- ne 2  2’lik kareye bölelim:

Eğer n = 12 olsaydı, karemizi 16 tane 3 × 3 boyutlu küçük kareye bölecektik.

Şimdi her iki çaprazı da içeren m × m’lik karelere bakalım.

m kaç olursa olsun, bu karelerden 8 tane vardır. Yani 16 adet m × m’lik küçük karenin yarısı çaprazları içerir, öteki yarısı içermez. Bu kareleri kurşun kalemle boyayalım. n = 8 olduğun- da durum şöyle:

Şimdi her kareye bir sayı koyacağız. En üst sol köşeden ve 1’den başlayarak kareleri sırayla numaralayalım. Ancak gri ka- releri atlayalım, onları daha sonra numaralayacağız. n = 8 için elde ettiğimiz durumu gösterelim:

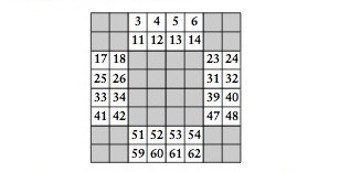
Şimdi sıra gri karelerde. Gri kareleri numaralamak için ay- nı şeyi yapacağız. Bu kez alt sağ köşeden başlayacağız ve beyaz kareleri atlayacağız. n = 8 iken gri karelerin numaraları şöyle olacak:

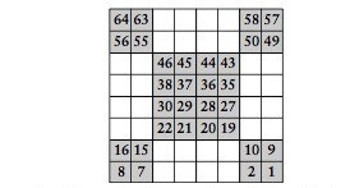
Yukardaki son iki şekli üstüste koyacak olursak birkaç sayfa önce verdiğimiz 8 x 8’lik sihirli kareyi elde ederiz.

Bu yöntemle 4m x 4m’lik her sihirli kareyi bulabiliriz.

12 x 12’lik sihirli kareyi de bulabiliriz. İşte bütün ihtişamıyla o sihirli kare:

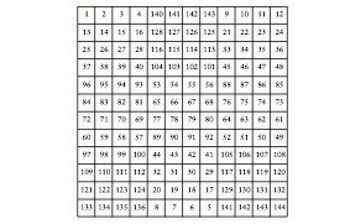
Şimdi sıra dörde bölünemeyen çift boyutlu sihirli kare yap- maya geldi.

Önce 6 x 6’lık sihirli kare yapmaya çalışalım.

Bir önceki yazımızda (sayfa 158) n x n’lik bir sihirli karenin sihirli sayısının, yani ya bir sıranın ya bir sütunun ya da bir çaprazın sayılarının toplamının n(n²+1)/2 olduğunu görmüştük. Bu formülde n = 6 alırsak 111 buluruz. Demek ki 6 x 6’lık bir sihirli karenin sihirli sayısı 111. Bu sayıyı aklımızın bir köşesine yazalım.

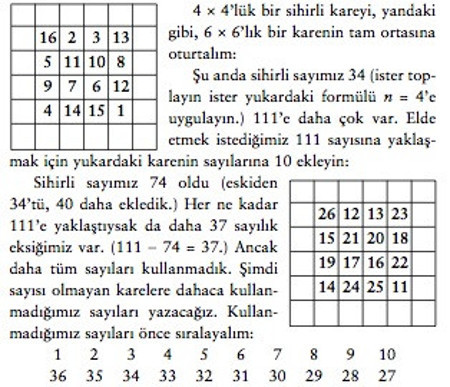
Sayısız karelerimize bu sayılardan yerleştireceğiz. Sıralama- ya dikkat edin. İkinci sıra tersten yazılmış ve altalta gelen sayıların toplamı 37. Demek ki üst sıradaki küçük sayının yeri alt sıradaki büyük sayının yerini belirleyecek.

Her kenarda 6 kare var. Bu 6 karenin yarısına üst sıradaki küçük sayılardan, geri kalan yarısına da alt kattaki büyük sayılardan koyacağız.

Önce çaprazların işini bitirelim. Üst iki köşe kareye dahaca kullanmadığımız en küçük iki sayıyı, 1 ve 2 sayılarını koyalım. Alt iki köşeye gelecek sayılar şimdi belli: 35 ve 36:

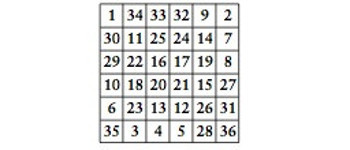
Böylece çaprazların toplamı 111 oldu. Bundan sonrası için bir kural olduğunu sanmıyorum. Çeşitli olasılıkları denemek gerekiyor. Ancak iki noktaya dikkat edelim: a) Her dört kena- ra üç büyük, üç küçük sayı koyacağız ve b) Karşılıklı sayıların toplamı 37 olacak. Elbet sihirli sayıyı da unutmayalım.

Alt sıraya daha hiç küçük sayı koymadık. Oysa üç küçük sayı koymamız gerekiyor. 3, 4 ve 5’i deneyelim. Bakalım ola- cak mı? Bu sayıların tepelerine 34, 33 ve 32 gelmek zorunda. Gelsinler. Sihirli karenin tamamlanmasına az kaldı. Sihirli sayı 111 olduğundan, alt ve üst kenarlara gelecek son sayılar da belli. Geriye sağ ve sol kenarlara gelecek sekiz sayıyı bulmak kalıyor. El yordamıyla bulunabiliyor bu sayılar. Ve işte 6 x 6’lık sihirli kare aşağıda.

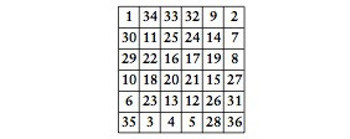
10 x 10’luk sihirli kare yapmak için,

1) 8 x 8’lik sihirli kareyi 10 x 10’luk karenin tam ortasına, göbeğine koyun.

2) Ortadaki 8 x 8’lik karenin her sayısına 18 ekleyin.

3) )Dahaca koymadığınız

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

100 99 98 97 96 95 94 93 92 91 90 89 88 87 86 85 84 83

sayılarını yukardaki biçimde bir kenara yazın.

4) Şimdi bu sayıları boş kalan kenar karelere yerleştireceğiz.

İlk olarak üst iki köşeye 1 ve 2 sayılarını, alt iki köşeye 100 ve 99 sayılarını yerleştirin.

5) Bundan sonrası için üç yardımcı kural var. Bu noktalar- dan yararlanarak 10  10’luk sihirli kareyi tamamlamaya çalı- şın:

5a) Her kenara 5 büyük, 5 küçük sayı yazılacak.

5b) Karşılıklı kenara toplamı 101 olan sayılar gelecek.

5c) Sihirli sayımız 505.

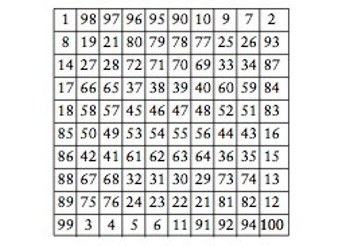
İşte bu yolla yapılmış 10 x 10’luk sihirli kare:

Genel yöntem aşağı yukarı belli olmuştur sanırım. Eğer n = 4m + 2, dörde bölünemeyen bir çift sayıysa, n x n boyutlu bir sihirli kare yapmak için:

1) n x n boyutlu karenin tam ortasına 4m x 4m’lik bir si- hirli kare yerleştirin.

2) Bu sihirli karenin her sayısına 2n – 2 ekleyin.

3) Dahaca kullanmadığınız sayıları iki sıra olarak yazın. Üste küçük sayıları küçükten büyüğe, alta büyük sayıları bü- yükten küçüğe koyun. Böylece üstüste gelen sayıların toplamı n²+ 1 olacaktır. Bu sayıları kenardaki boş karelere yerleştire- ceksiniz.

4) İlk olarak 1 ve 2 sayılarını üst kenar köşelerine yerleştirin. Alt köşelere n²– 1 ve n²sayıları gelecek.