Bir oyun
Bu oyun, başarıya ulaşırsa, ancak n2 + 2n hamlede başarıya ulaşır.

Oyunumuz n siyah ve n beyaz taşla ve tek başına oynanır. Taşlar 2n + 1 yuvalı bir tahtanın üstüne şöyle yerleştirilir. (Aşağıdaki örnekte n = 2.)
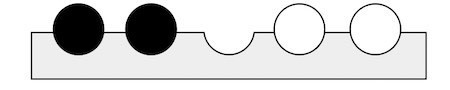
n siyah taş en sola, n beyaz taş en sağa... Ortada da boş bir yuva bırakılır.
Oyunun kuralları şöyle:
1) Her hamlede tek bir taşa dokunulur.
2) İki tür hamle var: a) bir taş, sağa ya da sola bir hane kaydırılabilir, b) bir taş, arkası boş karşıt renkli tek bir taşın üstün- den atlatılabilir.
3) Amaç, yukardaki pozisyonun tam simetriğini, yani aşağıdaki pozisyonu elde etmektir:
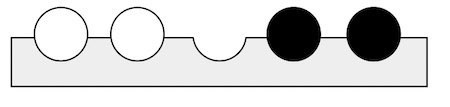
Pek o kadar zor bir oyun değil. İşte n = 2 olduğunda çözüm:
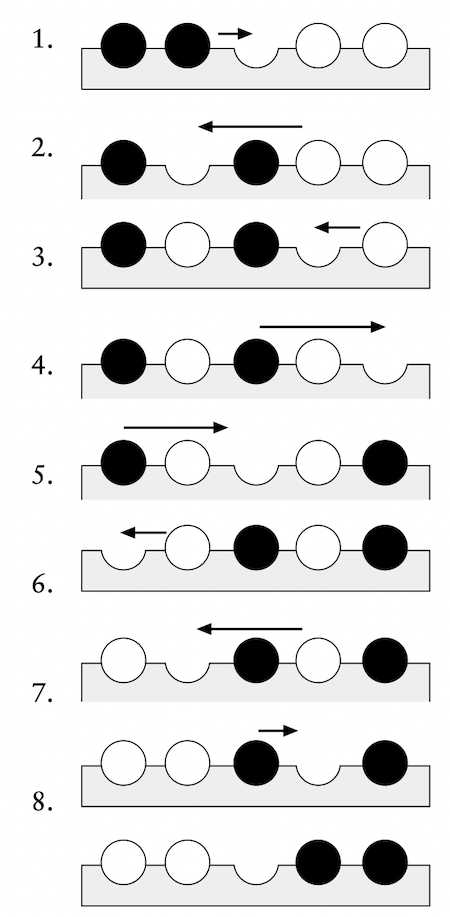
Yukarda da görüleceği üzere, n = 2 iken sekiz hamlede oyunu bitirebiliyoruz. Daha az hamlede de bitmez bu oyun.
Genel olarak 2n taşla oynanan oyun en az kaç hamlede biter? Hatta biter mi?
Her şeyden önce oyunun n2 + 2n hamleden önce bitmeyeceğini kanıtlayalım. Aynı renk taşlar birbirinin üstünden atlayamayacağından, taşlar ancak sıralarını koruyarak öbür yakaya gidebilirler. Örneğin, en soldaki siyah taş, öbür tarafta gene en soldaki siyah taş olmalı. Dolayısıyla her taş n + 1 uzaklığa gitmeli. Demek ki hiç atlama olmazsa, 2n taş toplam 2n(n + 1) hamle yapmalı. Ama atlama olacak. Ne kadar atlama olacak? Ne kadar siyah-beyaz taş karşılaşması olursa o kadar atlama olacak. Her siyah taş her beyaz taşla kesinlikle karşılaşacak. Demek ki her siyah taş n kez beyaz taşlarla karşılaşacak. Top- lam n siyah taş olduğundan, karşılaşma sayısı n2. Her karşılaşma bize bir hamle tasarruf ettiriyor. Demek ki hamle sayımız 2n(n + 1) - n2 sayısından, yani n2 + 2n sayısından daha az olamaz.
Eğer geriye gitmek yasaksa, o zaman bu oyun - başarıya ulaşırsa - ancak bu kadar hamlede başarıya ulaşır. Geriye gitmek de bu oyunda gereksizdir, hiçbir işe yaramaz, yani geriye gitmekle bir önceki hamleyi geri almak aynı şeydir. Dolayısıyla bu oyun, başarıya ulaşırsa, ancak n2 + 2n hamlede başarıya ulaşır.
Peki, bu oyun başarıya ulaşır mı? Bunu kanıtlamak pek o kadar kolay değil galiba.
n = 3 iken oyunu oynayın, oyunu başarmanın pek o kadar da kolay olmadığını göreceksiniz (siyah topları A, beyaz topları B gösterdik):
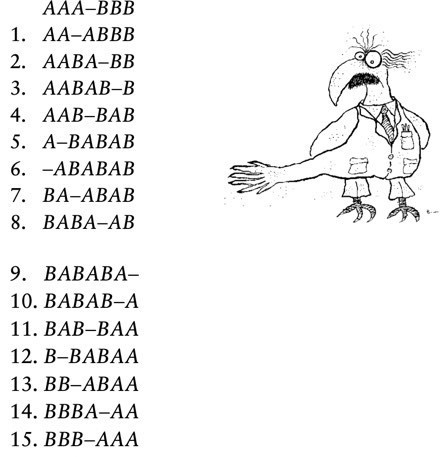
Örneğin yukardaki ikinci hamleden sonraki pozisyon AA- BA-BB ve o aşamada B yerine A’yı oynatmak hatadır, üç ham- le sonra oyun tıkanır.
Dört taşla daha zor kazanmak. Yirmi taşla, çok çok zor ol- malı...
Evet. Bu oyunun başarıyla sonuçlanabileceğini kanıtlamak gerekiyor, hem de hiçbir taş geri gitmeden...
Ayrıca mümkünse oyunun nasıl oynandığında kazanılacağını, yani kazanma algoritmasını bulmak gerekiyor. Yirmi taş- la nasıl oynamalı da kazanmalı?
Şimdi şuna dikkat edelim: Oyunun her anında beyazların en fazla bir hamlesi vardır. Aynı biçimde siyahların da en fazla bir hamlesi vardır. Her ne kadar hem siyahların hem de beyazların birer hamlesi olabiliyorsa da, oyunun bir anında aynı rengin iki değişik hamlesi olamaz. Bunu aklımızda tutalım.
Yukardaki n = 2 ve n = 3 için oyunu nasıl oynadığımıza ba- kalım.
n = 2 için oyun nasıl oynanmış? Bir kere siyah, iki kere be- yaz... Siyah yerine A, beyaz yerine B diyecek olursak, bu oyunu, 1 kere A 2 kere B 3 kere A 3 kere B 3 kere A 2 kere B 1 kere A oynamış. Yani oyun, 1A, 2B, 3A, 3B, 3A, 2B, 1A biçiminde cereyan etmiş. Bunu 1, 2, 3, 3, 3, 2, 1 olarak da gösterebiliriz.
n = 3 için oyun nasıl oynanmış? Bakalım. Bu oyun 1, 2, 3, 4, 4, 4, 3, 2, 1 biçiminde oynanmış. Yani bir kere A, iki kere B, üç kere A... oynamış.
Genel olarak oyunu kazanma algoritması bu olmalı. 2n taşlı bir oyun,
1, 2, ..., n - 1, n, n, n, n - 1, ..., 2, 1
biçiminde oynanırsa başarıya ulaşır gibi geliyor bana. Yani bir kere A, iki kere B, üç kere A... oynayarak.
Neden böyle? Bilmiyorum, kanıtlayamadım.









